А. Горчаков. Примеры применения статистических методов при построении торговых алгоритмов
Доклад на семинаре ЭВОЛЮЦИОННЫЕ ПРОЦЕССЫ В ЭКОНОМИКЕ в Финансовом университете при Правительстве РФ 1.12.10
Идеальная «торговая система»
Пусть
O
t - цена открытия в день t;
С
t - цена закрытия в день t;
H
t - максимальная цена в день t;
L
t - минимальная цена в день t.
Идеальная торговая система «только лонг»
Если позиция на конец дня t-1 аут и С
t>O
t и (H
t+L
t)>(H
t-1+L
t-1), то входим в лонг по максимуму из двух цен: O
t и (H
t+L
t)/2;
Если позиция на конец дня t-1 лонг и С
t<O
t, то выходим из лонга по минимуму из двух цен: O
t и (H
t+L
t)/2.
Сейчас я уже не вспомню, каким образом нашел эту «систему» весной 1998-го, когда начинал построение своих первых систем, но точно помню, что она меня поразила тем, что была достаточно устойчивой, как на акциях индексного фонда SPRD (тикер SPY
*) с 1990-го года, так и на акциях РАО ЕС России (тикер EESR) и Газпрома (тикер GAZP) с 1996-го года. И при этом соотношение «доходность-риск» на всех трех эмитентах было примерно одинаково, а риск пропорционален стандартному отклонению первых разностей логарифмов цен закрытия.
Готовясь к этому семинару, я решил проверить результаты этой «системы» в кризис 2008-го года на данных SPY с 09.10.2007 (локальный максимум после «кризиса доткомов» 2000-го года) по 09.03.2009 (минимум SPY на «ипотечном кризисе» 2008-го года)

Удивительно, но
мое управление в этот период показало максимальную просадку 22.10.08 (-18,8% (=-22,6%/1,2)), а новый максимум счета был достигнут на закрытии дня 29.10.08 (напомним, что 27.10.08 в России, в отличие от США, торги не проводились)
*акции фонда взяты потому, что в данных по индексу S&P500 открытие обычно устанавливается равным закрытию предыдущего дня, что исключает из данных междневные гепы и де-факто предполагает в торговом диапазоне дня наличие цен, по которым не совершались реальные сделки.
Как мы видим, для построения торговых моделей, приближающих эту «систему» нам требуется построить два как можно более точных статистических прогноза: прогноз завтрашних цен (H+L) и прогноз либо завтрашнего цвета свечи, либо сегодняшнего, но в начале торгового дня. Для первого прогноза нам потребуется модель ценообразования на фондовом рынке.
Аргументы в пользу условно-нормальных моделей
Гипотеза: первая разность логарифмов цен ликвидных акций за достаточно большой промежуток торгов имеет нормальное распределение, т. е.
ln С
t/C
t-1=a
t+
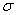
•s
t•n
t, где n
t ~ N(0,1), (1)
Аргументы в пользу этой гипотезы:
1. Первая разность логарифмов цен ликвидных акций за достаточно большой промежуток торгов является суммой большого числа первых разностей логарифмов тиков;
2. Каждый тик является действием двух или нескольких трейдеров: трейдера, решившего купить по оферам или продать по бидам и трейдера (-ов), поставивших эти биды (офера);
3. Два трейдера, пользующиеся полностью одинаковыми методами принятия решения – редкость;
4. Группы трейдеров, использующих «близкие» методы принятия решения, представляют собой о-малое (как по количеству, так и по объему средств) от корня из общего числа трейдеров и их объемов средств;
5. Любая группа трейдеров, использующих «близкие» методы принятия решения, не обладает достаточным объемом капитала для «существенного» изменения цены актива;
6. Для любого трейдера число трейдеров, использующих независимые или слабозависимые методы принятия решения, по порядку близко к множеству всех трейдеров.
Здесь под «трейдером» мы понимаем человека, принимающего решения о совершении сделок на бирже, в то числе и с использованием разработанных им «роботов».
Все это позволяет считать набор первых разностей логарифмов тиков ограниченными слабозависимыми случайными величинами по типу
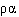
-зависимости, введенной в моей работе:
А. Б. Горчаков. Верхние оценки семиинвариантов суммы мультииндексированных случайных величин. Дискретная математика (1995), т. 7, вып. 3, с. 33-46
как обобщение ряда известных случаев слабой зависимости на случай случайных величин, у которых условия зависимости невозможно описать в терминах некой метрики на индексах суммирования (зависимость между методами принятия решения трейдерами тоже вряд ли можно подогнать под какую-либо метрику). Также в данной работе приведены достаточные условия асимптотической нормальности (даже в области больших уклонений) для сумм
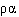
-зависимых случайных величин, которые хорошо перекликаются с приведенными пп. 1-6.
Немартигнальная модель ценообразования
С целью упрощения дальнейших выкладок и чтобы не множить сущности, предположим (как и в мартингальной модели), что последовательность n
t из (1) - последовательность независимых случайных величин (их одинаковую распределенность мы уже определили выше в рамках гипотезы об условной нормальности). Многочисленные исследования показали, что одномерные распределения ln С
t/C
t-1 имеют «тяжелые хвосты», что делает гипотезу a
t=const и s
t= const нежизнеспособной. Поэтому адекватное описание поведения цен на рынке условно-нормальной моделью лежит на пути отказа от одного или от обоих этих равенств. Современные мартингальные модели идут по пути отказа от равенства s
t= const с сохранением равенства a
t=const=«безрисковая ставка». При этом s
t обычно предполагается неким стационарным процессом (ARCH-модель и ее многочисленные обобщения), а временные «существенные» отклонения реальных первых разностей логарифмов цен от получающегося стационарного процесса объясняются сторонниками мартингальной теории изредко возникающими краткосрочными колебаниями «безрисковой ставки». Наше обобщение мартингальной модели будет состоять в том, что эти колебания a
t происходят достаточно часто и являются неотъемлемой частью динамики цен. Также мы несколько видоизменим и модель для s
t, синхронизовав ее колебания с колебаниями a
t.
Пусть дана стационарная ненаблюдаемая последовательность
(
D i,A
i,S
i), i=1, 2, …
где
D i - это последовательность независимых положительных целочисленных случайных величин, принимающих значения больше 1;
A
i - это процесс с отрицательной коррелированностью соседних величин;
S
i - это последовательность независимых неотрицательных одинаково распределенных случайных величин с некоторым унимодальным распределением с модой равной 1.
Пусть
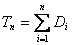
. Тогда для всех t из интервала
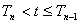
выполнены равенства a
t=А
n и s
t=S
n, т. е.
ln Ц
t/Ц
t-1=A
n+
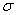
•S
n•n
t, (2)
Последовательности
D i, A
i («тренд»), S
i («волатильность») и n
t («шум») предполагаются независимыми между собой.
Первоначально автором рассматривалась модель
ln Ц
t/Ц
t-1=A
n+B
n•(t-T
n)+
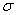
•n
t, где для любого n |A
n|>|B
n•(T
n+1-T
n)|, (3)
но после ряда исследований реальных цен от нее было решено отказаться в пользу модели (2), как более адекватно описывающей поведение цен.
Мы специально заменили в (2) латинскую букву С на русскую Ц, так как данное представление можно использовать не только для цен закрытия дня, обозначаемых ранее латинской буквой С, но и для других цен – H
t, L
t и (H
t+L
t)/2 (последовательности (A
i,S
i), i=1, 2, …, для каждой из цен могут быть индивидуальные и существенно отличаться от аналогичных последовательностей для других цен).
Отметим, что в рамках данной модели может быть и объяснены и факт наличия «тяжелых хвостов» (из-за наличия случайных величин A
n и S
n в представлении (2)) и факт близости к нулевой АКФ ln С
t/C
t-1 (из-за отрицательной коррелированности A
n).
Таким образом, в рамках нашей модели первые разности логарифмов цен уже представляют собой не стационарную последовательность, как в мартингальной модели, а нестационарный «отклик» на ненаблюдаемую стационарную последовательность.
Прогнозирование цен в рамках немартингальной модели (критерии «разладки»)
Нетрудно видеть, что в рамках приведенной модели для
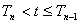
оптимальным в среднеквадратичном прогнозом
d i=ln Ц
t/Ц
t-1, i=t-Т
n является A
n. В свою очередь оптимальной несмещенной оценкой A
n является статистика
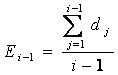
, i>2 (без учета отрицательной коррелированности в последовательности A
i). Так как при i<3 прогнозирование
d i невозможно, то де-факто задача прогноза
d i сводится в первую очередь к задаче выявления точек Т
n, известной в теории выделения сигнала на фоне шума, как задача о «разладке».
Также нетрудно видеть, что при i>2 статистика

имеет распределение Стъюдента с i-2 степенями свободы.
При i>2, если в момент времени i критерий «разладки», основанный на статистике (4), указал на «разладку» (при некотором уровне доверия), для подтверждения (или отмены) «разладки» в момент времени i+1 можно воспользоваться статистиками
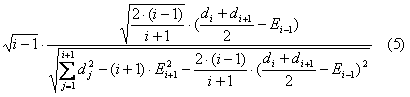
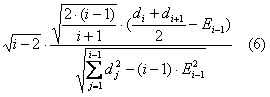
первая из которых имеет распределение Стъюдента с i-1 степенями свободы, а вторая - распределение Стъюдента с i-2 степенями свободы.
В общем случае выбор уровней доверия критериев «разладки» и между статистиками (5) и (6) – это вопрос оптимизации торговых систем, основанных на этих статистиках. Также открытым остается вопрос для каких цен строить данные статистики – только для (H
t+L
t)/2 (которые используются в идеальной «системе») или же использовать одновременно результаты для H
t, L
t, С
t и (H
t+L
t)/2 и на основе значений четырех статистик принимать торговые решения, путем кластеризации четырехмерного пространства значений статистик на состояния:
- лонг;
- аут.
чисто эмпирически через оценки условных вероятностей пар последовательных состояний.
В своей практической деятельности автор использует оба варианта, путем построения «портфеля систем» на одном эмитенте. Авторский метод оптимизации параметров систем с одновременным построением «портфеля систем» изложен в
докладе на II Ежегодной Конференции по системной торговле (июнь 2004)
Уточненная немартингальная модель цен
Удобство статистик (4)-(6) в том, что они инвариантны относительно распределений (
D i,A
i,S
i), однако в этом и состоит и их слабость – ошибки критериев (из-за «малых выборок») и основанных на них торговых систем порой бывают слишком часты, особенно в условиях выборочных оценок S
i намного меньше 1 («низкая волатильность»). Для получения более точных критериев требуется уточнение модели.
Как мы отмечали выше, S
i имеет некоторое унимодальное распределение с модой равной 1. В качестве такого распределения можно взять распределение с плотностью:
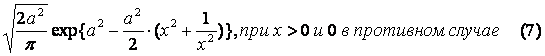
Тогда плотность распределения
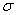
•S
n•n
t имеет вид

Отметим, что данное распределение является частным случаем обобщенного гиперболического распределения, активно применяемого в последние годы для не условно-нормального мартингального моделирования рядов первых разностей логарифмов цен. Также отметим, что это распределение имеет «тяжелые хвосты» со скоростью убывания
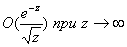
.
Явный вид плотности распределение
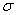
•S
n•n
t позволяет строить оценки максимального правдоподобия для
а2 и
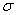
на всем имеющемся материале и использовать в знаменателях статистик (4)-(6) максимум из (оценка
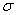
)•10% квантиль распределения с плотностью (7), полученный подстановкой оценки
a2, и значений статистик знаменателей, приведенных в (4)-(6). Это позволяет сократить ошибки торговых систем в условиях «низкой волатильности». К сожалению, оценки для
а2 и
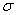
не выводятся в виде формул от элементарных функций, а являются решением системы дифференциальных уравнений, сводящейся к системе равенств нулю линейных комбинаций функций Макдональда и для каждого ряда цен находятся только алгоритмом поиска решения в Excel. Та же самая проблема возникает и при оптимизации систем, основанных на критерии «разладки» с использованием функции правдоподобия. Последняя функция выражается в виде сложного интеграла, затабулировать распределение которого в настоящее время не представляется возможным. Хотя из вида этой функции правдоподобия следует, что статистики, используемые в числителе и знаменателе статистик (4)-(6) являются достаточными статистиками. В соответствии с известной теоремой теории статистического оценивания получаем, что в данном случае оптимальные критерии находятся в классе функций от этих статистик, частным случаем которых являются статистики (4)-(6).
Прогнозирование внутридневных уровней
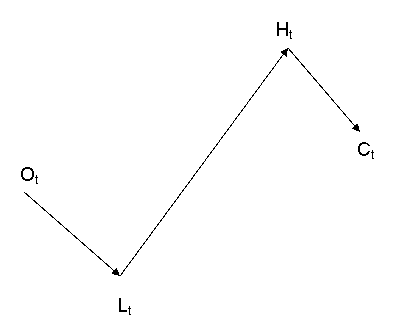
Итак, с помощью прогнозных оценок, построенных указанными выше методами, мы можем однозначно вычислить гипотетическую завтрашнюю цену М=(H+L)/2, выше(ниже) которой наши критерии не укажут на «разладку» или наоборот укажут на «разладку». Как это можно использовать при покупках внутри дня, да еще с одновременным прогнозом цвета свечи? Для этого рассмотрим «идеальное» движение цены внутри дня, которое выглядит следующим образом
Если С
t>O
t, то O
t->L
t->H
t->С
t
и наоборот если С
t<O
t, то O
t->H
t->L
t->С
t
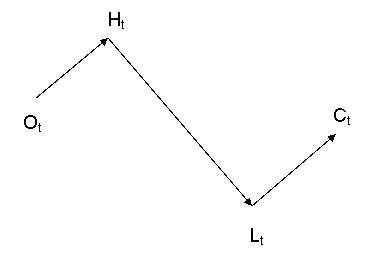
Данный вид движения делает хорошим прогнозом для уровня покупки (без учета цвета свечи) цену 2*М-текущий минимум, для уровня продажи - 2*М-текущий максимум. Прогноз цвета свечи несколько сложнее. Для него мы используем линейные взаимосвязи между lnC
t/O
t и lnН
t/O
t и lnO
t/C
t и lnO
t/L
t, оцениваемые на ценовой истории и при помощи них прогнозируем уровень цены вверх от открытия после которой падение ниже открытия к закрытию имеет пониженную вероятность (при текущей позиции аут) или уровень цены вниз от открытия после которой рост выше открытия к закрытию также имеет пониженную вероятность (при текущей позиции лонг). Упомянутый уровень вероятности закрытия ниже( выше) открытия также является оптимизируемым параметром систем. Теперь, беря максимум из двух упомянутых прогнозов «цены вверх» мы устанавливаем его в качестве уровня покупки и, соответственно, беря минимум из двух прогнозов «цены вниз», мы устанавливаем его в качестве уровня продажи (как уже упоминалось, в зависимости от позиции нам достаточно считать только один из двух уровней). Данный подход приводит к тому, что на свечах с «длинным телом», мы покупаем или продаем лучше цены (H
t+L
t)/2, а на свечах с «коротким телом» и «длинными хвостами» мы покупаем или продаем хуже цены (H
t+L
t)/2 (на свечах с «коротким телом» и «короткими хвостами» сделки, если и совершаются, то по ценам, близким к ценам закрытия и сказать, что-либо про «лучше-хуже» - сложно).
Как показала реальная практика, варьируя параметры систем и предполагая, что во все дни имеют место только «идеальные» движения, можно добиться в среднем совершения сделок не хуже теоретической цены идеальной «системы». Однако не все в нашем мире идеально, а в дни с неидеальным движением цены системы, подобные нашим, могут совершать убыточные сделки (продал-откупил дороже, купил-продал дешевле), так как по своей логике построения внутридневный уровень покупки всегда выше уровня продажи. Поэтому, прежде, чем применять подобные системы на конкретном эмитенте, не мешает удостовериться, что в нем на истории доля дней с «идеальным» движением цены была не ниже 70% и потом оптимизировать уровни вероятностей (критериев, основанных на статистиках (4)-(6) и уровень вероятности для внутридневных прогнозов «цены вверх» и «цены вниз») на конкретной внутридневной динамике цен данного эмитента.
И в заключении приведем результаты исследований «идеальности» внутридневных движений для американского рынка, которые проводились в 2001-2002-м годах. Как показали эти исследования, высокая доля «идеальных» внутридневных движений (более 70%) присуща индексообразующим «голубым фишкам» (
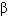
с S&P500 не ниже 0,5) с ценой не ниже 30$ за акцию (для Германии аналогичный порог по исследованиям 2005 года акций, входящих в индекс DAX, составил ~25€). В то же время для акций ценой ниже 10$ эта доля становится крайне малой (вероятней всего, это связано с тем, что волатильность для дешевых акций надо измерять не по первым разностям логарифмов цен, а по первым разностям самих цен и соответствующим образом перестраивать модель ценообразования). Поэтому на падающем рынке акции, упавшие в цене с 30-40$$ до 20$ (с 25-30€ € до 15€ для Германии), лучше исключить из торгуемого по подобным системам портфеля, даже несмотря на наличие текущей системной просадки в этих акциях и высокой оценки вероятности ее отыгрыша, полученной по историческим данным.



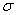 •s t•n t, где n t ~ N(0,1), (1)
•s t•n t, где n t ~ N(0,1), (1)
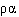 -зависимости, введенной в моей работе:
-зависимости, введенной в моей работе:
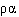 -зависимых случайных величин, которые хорошо перекликаются с приведенными пп. 1-6.
-зависимых случайных величин, которые хорошо перекликаются с приведенными пп. 1-6.
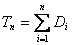 . Тогда для всех t из интервала
. Тогда для всех t из интервала 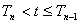 выполнены равенства a t=А n и s t=S n, т. е.
выполнены равенства a t=А n и s t=S n, т. е.
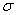 •S n•n t, (2)
•S n•n t, (2)
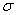 •n t, где для любого n |A n|>|B n•(T n+1-T n)|, (3)
•n t, где для любого n |A n|>|B n•(T n+1-T n)|, (3)
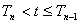 оптимальным в среднеквадратичном прогнозом d i=ln Ц t/Ц t-1, i=t-Т n является A n. В свою очередь оптимальной несмещенной оценкой A n является статистика
оптимальным в среднеквадратичном прогнозом d i=ln Ц t/Ц t-1, i=t-Т n является A n. В свою очередь оптимальной несмещенной оценкой A n является статистика 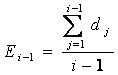 , i>2 (без учета отрицательной коррелированности в последовательности A i). Так как при i<3 прогнозирование d i невозможно, то де-факто задача прогноза d i сводится в первую очередь к задаче выявления точек Т n, известной в теории выделения сигнала на фоне шума, как задача о «разладке».
, i>2 (без учета отрицательной коррелированности в последовательности A i). Так как при i<3 прогнозирование d i невозможно, то де-факто задача прогноза d i сводится в первую очередь к задаче выявления точек Т n, известной в теории выделения сигнала на фоне шума, как задача о «разладке».

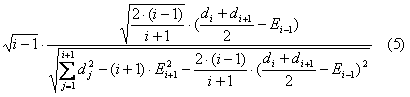
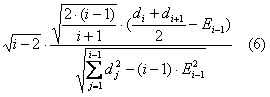
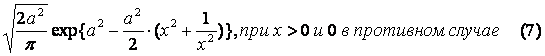
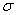 •S n•n t имеет вид
•S n•n t имеет вид

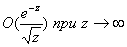 .
.
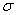 •S n•n t позволяет строить оценки максимального правдоподобия для а2 и
•S n•n t позволяет строить оценки максимального правдоподобия для а2 и 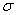 на всем имеющемся материале и использовать в знаменателях статистик (4)-(6) максимум из (оценка
на всем имеющемся материале и использовать в знаменателях статистик (4)-(6) максимум из (оценка 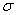 )•10% квантиль распределения с плотностью (7), полученный подстановкой оценки a2, и значений статистик знаменателей, приведенных в (4)-(6). Это позволяет сократить ошибки торговых систем в условиях «низкой волатильности». К сожалению, оценки для а2 и
)•10% квантиль распределения с плотностью (7), полученный подстановкой оценки a2, и значений статистик знаменателей, приведенных в (4)-(6). Это позволяет сократить ошибки торговых систем в условиях «низкой волатильности». К сожалению, оценки для а2 и 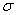 не выводятся в виде формул от элементарных функций, а являются решением системы дифференциальных уравнений, сводящейся к системе равенств нулю линейных комбинаций функций Макдональда и для каждого ряда цен находятся только алгоритмом поиска решения в Excel. Та же самая проблема возникает и при оптимизации систем, основанных на критерии «разладки» с использованием функции правдоподобия. Последняя функция выражается в виде сложного интеграла, затабулировать распределение которого в настоящее время не представляется возможным. Хотя из вида этой функции правдоподобия следует, что статистики, используемые в числителе и знаменателе статистик (4)-(6) являются достаточными статистиками. В соответствии с известной теоремой теории статистического оценивания получаем, что в данном случае оптимальные критерии находятся в классе функций от этих статистик, частным случаем которых являются статистики (4)-(6).
не выводятся в виде формул от элементарных функций, а являются решением системы дифференциальных уравнений, сводящейся к системе равенств нулю линейных комбинаций функций Макдональда и для каждого ряда цен находятся только алгоритмом поиска решения в Excel. Та же самая проблема возникает и при оптимизации систем, основанных на критерии «разладки» с использованием функции правдоподобия. Последняя функция выражается в виде сложного интеграла, затабулировать распределение которого в настоящее время не представляется возможным. Хотя из вида этой функции правдоподобия следует, что статистики, используемые в числителе и знаменателе статистик (4)-(6) являются достаточными статистиками. В соответствии с известной теоремой теории статистического оценивания получаем, что в данном случае оптимальные критерии находятся в классе функций от этих статистик, частным случаем которых являются статистики (4)-(6).


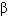 с S&P500 не ниже 0,5) с ценой не ниже 30$ за акцию (для Германии аналогичный порог по исследованиям 2005 года акций, входящих в индекс DAX, составил ~25€). В то же время для акций ценой ниже 10$ эта доля становится крайне малой (вероятней всего, это связано с тем, что волатильность для дешевых акций надо измерять не по первым разностям логарифмов цен, а по первым разностям самих цен и соответствующим образом перестраивать модель ценообразования). Поэтому на падающем рынке акции, упавшие в цене с 30-40$$ до 20$ (с 25-30€ € до 15€ для Германии), лучше исключить из торгуемого по подобным системам портфеля, даже несмотря на наличие текущей системной просадки в этих акциях и высокой оценки вероятности ее отыгрыша, полученной по историческим данным.
с S&P500 не ниже 0,5) с ценой не ниже 30$ за акцию (для Германии аналогичный порог по исследованиям 2005 года акций, входящих в индекс DAX, составил ~25€). В то же время для акций ценой ниже 10$ эта доля становится крайне малой (вероятней всего, это связано с тем, что волатильность для дешевых акций надо измерять не по первым разностям логарифмов цен, а по первым разностям самих цен и соответствующим образом перестраивать модель ценообразования). Поэтому на падающем рынке акции, упавшие в цене с 30-40$$ до 20$ (с 25-30€ € до 15€ для Германии), лучше исключить из торгуемого по подобным системам портфеля, даже несмотря на наличие текущей системной просадки в этих акциях и высокой оценки вероятности ее отыгрыша, полученной по историческим данным.