Когда речь идёт о прогнозе в финансовой сфере, большинство людей задают себе вопрос, а возможно ли это? И они совершенно правы – решение вопроса о возможности прогноза в области экономики является важным для всей индустрии финансовой аналитики. У практиков, пытавшихся применить «в лоб» математические методы, складывается пессимистическое мнение по поводу возможности прогноза. Некоторые даже категорически высказываются о его невозможности. Понять причину такого единодушного пессимизма нетрудно: для прямого извлечения финансовой или экономической выгоды точности прогноза, как правило, не хватает. Этот тезис, являющийся основой для позиций скептиков, переводит вопрос из плоскости «возможно – невозможно» в плоскость достаточной точности прогноза «точность достаточна – точность недостаточна». Это очень важный момент. Речь уже не идёт о принципиальной невозможности прогноза, речь идёт о приемлемой для практического использования точности.
Как и в других естественнонаучных областях, чтобы отслеживать изменение какого-то свойства, нужно уметь его измерять. В нашем случае под свойством понимается точность прогноза, а различного рода ошибки являются численным выражением этого свойства. Таким образом, исходный вопрос сводится к вопросу: «Как измерить точность прогноза?». И на первый взгляд, как это обычно и бывает, никаких проблем с ответом нет.

Статистические свойства среднеквадратичной ошибки.
Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру.
А. Эйнштейн

Проблема измерения качества прогноза станет очевидной, если оценить содержательность статистических выводов, следующих из расчета классических мер ошибок. Обратимся, для примера, к одной из наиболее распространенных мер – среднеквадратичной ошибке RMSE (Root Mean Square Error). Известно, что в случае, когда приращения цены – независимы и распределены по нормальному закону, величина RMSE и среднее приращений  являются оценками максимального правдоподобия неизвестных параметров этого нормального распределения: σ и μ соответственно. Известно также, что такие оценки параметров нормального распределения обладают свойством состоятельности: вероятность расхождения между оценкой и истинным значением параметра на любую, сколь угодно малую величину, стремится к нулю с ростом числа наблюдений. Последнее свойство, несмотря на случайный характер наблюдений, позволяет с любой заданной точностью восстановить закон распределения ошибки. Для этого нужно подставить в формулу для нормальной плотности распределения оценки параметров вместо их реальных значений. После этого становится доступной вся статистическая информация об ошибке: моменты, квантили, доверительные интервалы. Часто применяется, например, такой результат:
- вероятность попадания ошибки в интервал delta–RMSE...delta+RMSE составляет приближенно 68.3 % (правило 1-sigma);
- вероятность попадания ошибки в интервал delta–2*RMSE... delta+2∙RMSE составляет приближенно 95.5 % (правило 2-sigma);
- вероятность попадания ошибки в интервал delta–3*RMSE... delta+3∙RMSE составляет приближенно 99.7 % (правило 3-sigma).
Допустим теперь, что гипотеза о нормальном распределении ошибки неверна. В этом случае RMSE^2 – не более чем одна из оценок дисперсии распределения. Информации, содержащейся в RMSE, уже недостаточно для восстановления распределения, оценки квантилей и построения доверительных интервалов произвольного уровня. Однако, известен замечательный эмпирический результат: для широкого ряда практически встречаемых распределений в качестве хорошего приближения 90%-го доверительного интервала может быть использован интервал delta–1.6* RMSE... delta+1.6*RMSE (правило 1.6-sigma). Построение доверительных интервалов другого уровня требует применения алгоритмов оценки функции распределения или плотности ошибки. Формальный перенос свойств, справедливых в предположении нормальности ошибки, в общем случае приводит к некорректным статистическим выводам. Так, применение правила 1-sigma для построения 68%-го доверительного интервала может привести к недооцененной (рис.А) и переоцененной (рис.B) вероятности малых ошибок. В свою очередь, завышенная вероятность малых ошибок в прогнозе финансовых рядов ведет к недооценке рисков.

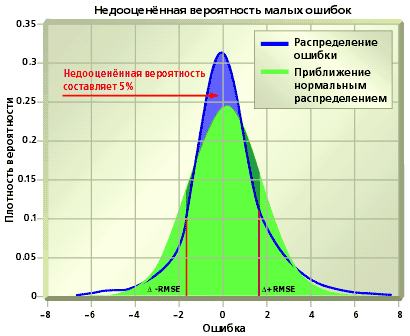
Рис.А. Применение RMSE к построению доверительного интервала: заниженная (недооценённая) вероятность малых ошибок.

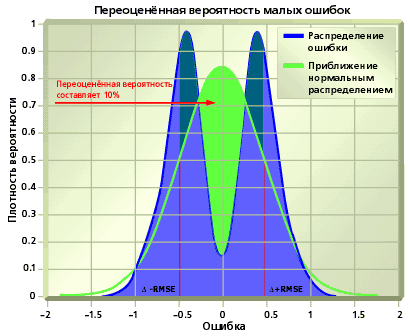
Рис.B. Применение RMSE к построению доверительного интервала: завышенная (переоценённая) вероятность малых ошибок.

Отметим, что причиной недооцененных рисков может быть и сама структура RMSE: интегральный характер меры приводит к тому, что информация об экстремальных значениях ошибки представлена в RMSE слабо и возможны значительные по величине, но редкие, выходы ошибки прогноза за пределы доверительного интервала, построенного с использованием RMSE. При невысокой частоте подобных событий потери от недооцененного риска, тем не менее, во многих случаях превышают позитивный баланс, накопленный за длительный период использования прогноза.

Некоторые свойства максимальной абсолютной ошибки.
С позиции использования в финансовых приложениях более предпочтительными могут быть оценки, которые несколько завышают риски. Меньшая доходность в этом случае компенсируется отсутствием экстремально больших потерь. Классической мерой ошибок, приводящей к подобным оценкам, является максимальная абсолютная ошибка – MAE (Maximum Absolute Error).
В отличие от меры RMSE, где вес одного наблюдения убывает пропорционально объему выборки, вес отдельного наблюдения в оценке MAE равен единице и не уменьшается с ростом количества наблюдений. По этой причине величина MAE в значительно большей степени, чем RMSE, зависит от случайного характера наблюдений за ошибкой. Компенсировать эту зависимость можно только за счет большего числа наблюдений, используемых при расчете МАЕ.
Количество наблюдений, необходимых для расчета мер ошибок, можно оценить, если известен их закон распределения. Здесь следует напомнить: поскольку наблюдения за ошибкой являются случайными величинами, то мера ошибки также является случайной величиной, для которой можно найти закон распределения, вычислить среднее значение и построить доверительный интервал. Статистические характеристики величины ошибки зависят от количества наблюдений, используемых при ее расчете. Говорить о независимости оценки меры от конкретной реализации ошибок можно лишь в том случае, когда для данного количества наблюдений разброс значений меры, по крайней мере, не превосходит ее среднего значения. А ещё лучше, если интервал разброса составляет менее половины ожидаемого значения. Ниже приведены графики (рис. 1, 2, 3), которые показывают, как с увеличением объема выборки изменяется отношение длины 95%-го доверительного интервала к среднему значению меры ошибки. Графики построены в предположении, что наблюдения за ошибкой независимы и распределены по стандартному нормальному закону.

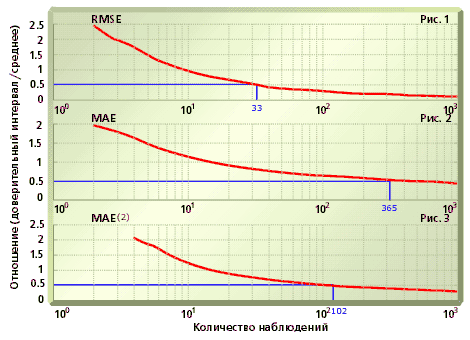
Рис. 1-3. Зависимость точности оценки от величины выборки.

Из графиков видно, что относительно небольшое отношение 1: 2 для RMSE обеспечивают около 30 наблюдений, а для MAE – более 350. Данный результат отражает проблему набора данных для вычисления меры MAE: выборки малого объема не позволяют избежать зависимости от конкретной реализации наблюдений за ошибкой, а в выборках большого объема возможно значительная неоднородность наблюдений по распределению (см. статью «Дыхание рынка»).
В некоторой степени решить проблему большого числа наблюдений, необходимых для расчета MAE, позволяет её модификация МАЕ(2) – для этого нужно рассмотреть второй по величине максимум модуля разности прогноза и реального значения. В общем случае, замена первого минимума и максимума на, соответственно, k-тый минимум и максимум уменьшает разброс значений модифицированной меры, чем и объясняется снижение требований к объему выборки. Кроме того, MAE(k) обладает свойством фильтрации: мера не чувствительна к наличию выбросов в наблюдениях за ошибкой, если количество выбросов не превышает k-1.
Рис.1 содержит график отношения длины доверительного интервала к среднему значению MAE(2) в зависимости от объема выборки. Сопоставление этого рисунка с рис.2 показывает, что количество наблюдений, обеспечивающих отношение 1:2 уменьшается более чем втрое, по сравнению со стандартной мерой MAE. Однако полностью проблему больших выборок введение модифицированной меры не решает, поскольку дальнейшее увеличение номера меры (k) приводит к тому, что по свойству оценки риска MAE(k) приближается к RMSE.
Помимо проблемы расчета меры, как и в случае RMSE, имеется проблема применения MAE и ее модификаций для построения доверительных интервалов. Без знания закона распределения наблюдений за ошибкой, вероятность попадания ошибки в интервалы, построенные с использованием MAE и MAE(k) не известна. Например, неверно считать равной единице вероятность попадания ошибки в интервал –MAE … MAE, поскольку этот вывод основан только на одной реализации наблюдений за ошибкой.
Подводя итог обсуждению мер RMSE и MAE, подчеркнем их основные недостатки: если неизвестен закон распределения ошибки, меры не могут быть оценены с заданной точностью и, главное, не дают представления о статистических свойствах ошибки прогноза. Преимущества мер связаны с решением задачи о распределении ошибки: когда закон распределения известен, информации, содержащейся в RMSE, MAE и модификациях MAE, достаточно для оценки его надежности.
Теперь обратим внимание на то, что меры RMSE и MAE являются размерными величинами. В случае прогноза рядов различной природы или с различным порядком прогнозируемой величины данное свойство препятствует сравнительному анализу ошибок. Простейшим решением вопроса является деление размерных (абсолютных) мер ошибки на любую величину той же размерности. В качестве делителя можно использовать, например, одно из наблюдений за прогнозируемой величиной или разность двух наблюдений. Наблюдения также могут быть заменены соответствующими значениями прогноза.
Отметим, что задача выбора нормирующего множителя достаточно нетривиальна. Так, в случае знакопеременных рядов, любой из выше приведенных делителей может мало отличаться или быть равным нулю, что влечет за собой большую погрешность в оценке относительной меры или, вообще, не позволяет получить оценку. Исключение близких к нулю значений является, при этом, не единственным требованием, которое предъявляется к делителю. Более подробно вопрос нормировки мер ошибок будет обсуждаться в следующих статьях.